Regular tilings of the 2D plane
I recently came across Euclidean tilings by convex regular polygons, which is super interesting. The problem is to fill the entire (infinite) 2D plane with non-overlapping regular polygons. The simplest case is to use a single regular polygon of fixed size - called Regular Tilings.
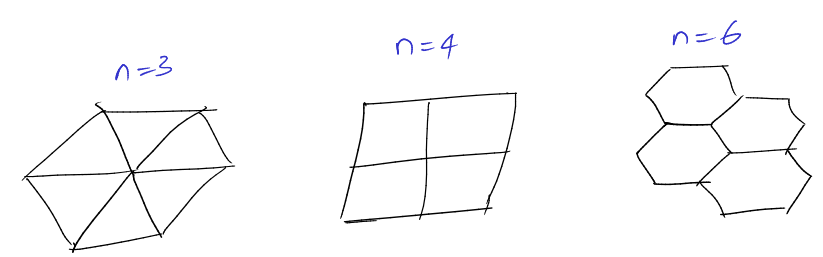
It turns out there are only three such tilings! With triangles $(n = 3)$ or squares $(n = 4)$ or hexagons $(n = 6)$.
§ Proof
Why is this so? I did some very minimal searching and did not find a proof, so here is my proof.

The internal angle has to be a multiple of $2\pi$. We know that the internal angle is $\theta = \frac{(n - 2)\pi}{n}$.
\[\theta \mid 2\pi \implies \frac{(n - 2)\pi}{n} \mid 2\pi \implies n - 2 \mid 2n \implies n - 2 \mid 2(n - 2) + 4 \implies n - 2 \mid 4\] \[\implies n - 2 \in \{1, 2, 4\} \implies n \in \{3, 4, 6\}\]Which proves that the only possible titlings are the ones listed above. To prove they actually exist, we just need a construction, which was done above.
§ Bonus
What are all the regular tilings of a 3D euclidean space? How do you about proving it?