ICPC WF 2020, Problem C. Domes
Solution and explanation for Problem C. Domes from the ICPC World Finals 2020, along with the implementation.
There is also a short video editorial from ICPCNews, with Borys Minaiev explaining the solution.
§ Problem
(Link) You have $n$ ($n \le 100$) monuments/points on a rectangular grid, and want to take a photo. Given some ordering of the monuments, find the are of the region, from which it is possible to take a photo, s.t. the monuments listed from left to right are in the given order.
§ A trivial solution
First we try to look for a trivial solution. We could consider all possible points, and test each one.
- One way to do this is by discretizing the grid. This is unfortunately too slow.
- Another is to randomly sample points, and take the ratio of valid samples to total samples. This unfortunately does not give enough precision.
But in both these approaches, we need a way to test if a point is valid or not. So let’s first figure that out.
§ Observation
Say we have selected a point $p$. Can we take a photo from $p$?
Just Two Points
Let us consider just two monuments, $A$ and $B$. Say $A$ should be to the left of $B$, when you take a photo from $p$. How do we check this?
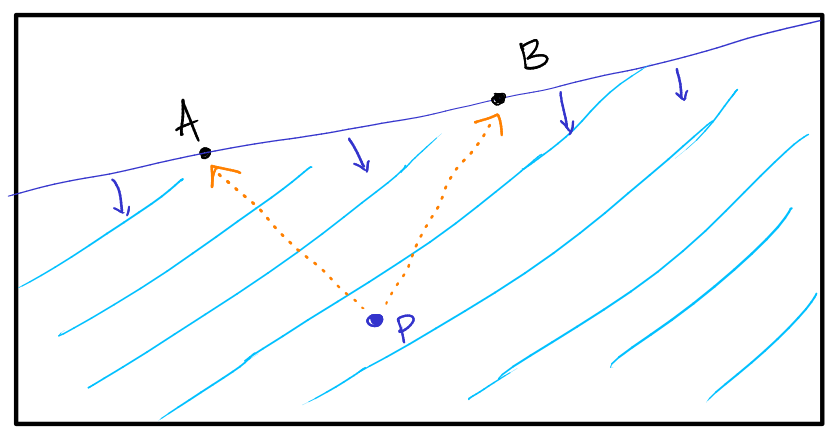
We can pick any point in the shaded region, and it is valid! That is, on the “right” or clockwise side of the line $AB$. This can be checked in $O(1)$ for a single point.
All points
To check for all points, we just take each pair and check the above constraint, whether $p$ lies in the corresponding shaded region. Totally $O(n^2)$ to check against all pairs.
§ Solution
This observation got us really close to the solution. All we need to do is take the common shaded region, over all the constraints. We need some primitive to implement half-plane intersection, and we are done.
This is a fairly straight-forward concept. After considering some constraints, we will have an open polygon. When cutting with a new line, it will remove some vertices and edges, and potentially add two more vertices, and an edge. So processing a constraint will be $O(n)$, and totally $O(n^3)$ for the entire solution.
§ Implementation
First, let us pull out our Point template.
template <class T>
bool isZero(T x) { return x == 0; }
const double EPS = 1e-9;
template <>
bool isZero(double x) { return fabs(x) < EPS; }
template <class T> struct Point {
typedef Point P;
T x, y;
explicit Point(T x = 0, T y = 0) : x(x), y(y) {}
bool operator<(P p) const { return tie(x, y) < tie(p.x, p.y); }
bool operator==(P p) const { return isZero(x - p.x) && isZero(y - p.y); }
P operator+(P p) const { return P(x + p.x, y + p.y); }
P operator-(P p) const { return P(x - p.x, y - p.y); }
P operator*(T d) const { return P(x * d, y * d); }
P operator/(T d) const { return P(x / d, y / d); }
T dot(P p) const { return x * p.x + y * p.y; }
T cross(P p) const { return x * p.y - y * p.x; }
T cross(P a, P b) const { return (a - *this).cross(b - *this); }
};
Now, for the solution, we need two primitives: Polygon Cut and Polygon Area.
// Line Intersection
template <class P>
pair<int, P> lineInter(P s1, P e1, P s2, P e2) {
auto d = (e1 - s1).cross(e2 - s2);
if (isZero(d)) // if parallel
return {-(s1.cross(e1, s2) == 0), P(0, 0)};
auto p = s2.cross(e1, e2), q = s2.cross(e2, s1);
return {1, (s1 * p + e1 * q) / d};
}
// Polygon Cut
typedef Point<double> P;
vector<P> polygonCut(const vector<P> &poly, P s, P e) {
if (poly.size() <= 2) return {};
vector<P> res;
for (size_t i = 0; i < poly.size(); i++) {
P cur = poly[i], prev = i ? poly[i - 1] : poly.back();
if (isZero(s.cross(e, cur))) {
res.push_back(cur);
continue;
}
bool side = s.cross(e, cur) < 0;
if (side != (s.cross(e, prev) < 0))
res.push_back(lineInter(s, e, cur, prev).second);
if (side)
res.push_back(cur);
}
return res;
}
// Polygon Area, returns twice the actual area, signed.
template <class T>
T polygonArea2(const vector<Point<T>> &v) {
T a = v.back().cross(v[0]);
for (size_t i = 0; i + 1 < v.size(); i++)
a += v[i].cross(v[i + 1]);
return a;
}
Once we have these, the solution is super simple!
int main() {
// input boundary dimensions and no. of monuments.
int dx, dy, n;
cin >> dx >> dy >> n;
// locations of monuments
vector<P> pts(n);
for (P &p : pts) cin >> p.x >> p.y;
// required permutation from left to right
VI perm(n);
for (int &x : perm) cin >> x, x--;
// the valid region polygon, initially the entire rectangle.
vector<P> poly;
poly.emplace_back(0, 0);
poly.emplace_back(0, dy);
poly.emplace_back(dx, dy);
poly.emplace_back(dx, 0);
// process all pairs, and cut off the left side of i->j
for (int i = 0; i + 1 < n; i++)
for (int j = i + 1; j < n; j++)
poly = polygonCut(poly, pts[perm[i]], pts[perm[j]]);
// final area
cout << setprecision(10) << fixed << fabs(polygonArea2(poly) / 2) << endl;
}